Rational for C#

Rational is ratio of 2 integers. It represents fractions of an integer. Most of the time if you deal with rational number, you can use real number (float) instead. But real number has an drawback. It cannot maintain proportion of 2 integers for number with repeating decimal. For example,

(1/20)² + (1/15)² - (1/12)²
= (1/400) + (1/225) - (1/144)
= (9/3600) + (16/3600) - (25/3600)
= 0

Now testing with real number:

double x = Math.Pow(1.0 / 20.0, 2.0);
double y = Math.Pow(1.0 / 15.0, 2.0);
double z = Math.Pow(1.0 / 12.0, 2.0);
Console.WriteLine(x + y - z);
//8.67361737988404E-19

Result is not zero as expected. To use rational, you can download from here. Rational class is required BigInteger in SilverLight package. You can construct rational several ways.

Rational a = new Rational(1, 20);
Rational b = (Rational)1 / 15;
Rational c = 1m / 12m;
Console.WriteLine(a.Power(2) + b.Power(2) - c.Power(2));
//0

You can construct rational using new keyword, first argument is numerator, and second argument is denominator. Second method is to cast from integer. Last method is to guess from decimal. Please noted that guessing rational from decimal may lose accuracy, such as:

Rational r = 1000001m / 600001m;
Console.WriteLine(r.ToString());
//5/3

You can see that it keeps 5/3 instead of 1000001/600001. If you need accuracy, construct rational or casting from integer are better solutions.

The Rational class always keep rational in reduced form, such as:

Rational r = (Rational)5 / 10;
Console.WriteLine(r.ToString());
//1/2

It keeps 1/2 instead of 5/10. This will make all same proportions such as 1/2, 3/6, 5/10 are all equivalent.

This Rational class supports infinity, negative zero, and not a number (NaN). This will make all arithmetic operations are equal to real number, such as:

//1/0 makes infinity
Rational inf = (Rational)1 / 0;
Console.WriteLine(inf);
//Infinity

//Invert of negative zero makes negative infinity
Rational nzero = (Rational)0 / -1;
Console.WriteLine(1 / nzero);
//-Infinity

//infinity - infinity = nan
Rational nan = inf - inf;
Console.WriteLine(nan);
//NaN

Let's test rational with an easy question from projecteuler.net.
Find numerator of the fraction immediately to left of 3/7 with denominator <= 1000000

Rational r = (Rational)3 / 7;
r -= (Rational)1 / 999999;
Console.WriteLine(r.Numerator);
//428570

Next topic is to create continued fractions from square root and generate sequence of rational.

Infinity, Negative Zero, and Not a Number

Mathematics always go beyond its own current dimension. Natural numbers was created, but it does not satisfy existence of zero and negative numbers. Integer was then created, but what happened if we scale integer into smaller numbers. Rational was then create, but it cannot represents number liked root of 2. Real numbers was then created, but some create Complex numbers to satisfy root of -1, and some create Extended real, to satisfy division of zero.

Extended real is very interesting, it doesn't comply with number system as following:

Infinity + 1 = Infinity
1 = Infinity - Infinity
1 = 0 ???

Therefore, infinity is not existed and division by zero is undefined. But extended real try to create its own rules by introducing non-number liked Infinity, Negative Infinity, Negative Zero, and Not a number.

Infinity can be created by 1/0. Some basic properties of infinity are:

1.0 / 0.0 = Inf
1.0 / Inf = 0.0
1.0 + Inf = Inf
Inf - Inf = NaN
Inf * 0.0 = NaN
Inf * -1.0 = -Inf

Infinity in extended real has its own sign. It can be positive or negative. Negative infinity can be created by -1/0. Some basic properties of negative infinity are:

-1.0 / 0.0 = -Inf
1.0 / -Inf = -0.0
1.0 / -0.0 = -Inf
1.0 + -Inf = -Inf
-Inf * -1.0 = Inf

Zero in extended real also has its own sign. It can be negative. Negative zero can be create by -0. Some basic properties of negative zero are:

-(0.0) = -0.0
-0.0 * -1.0 = 0.0
-0.0 * -0.0 = 0.0
-0.0 * 0.0 = -0.0
-0.0 + -0.0 = -0.0
-0.0 + 0.0 = 0.0
-1.0 % 1.0 = -0.0

All undefined numbers are Not a Number (NaN). All arithmatic operation with NaN result to NaN, therefore extended real has no arithmatic error. NaN can be created from:

0.0 / 0.0 = NaN
Inf - Inf = NaN
Inf * 0.0 = NaN
1.0 % 0.0 = NaN
Inf % 1.0 = NaN
Sqrt(-1.0) = NaN

Arithmatic comparisons for extended real are as follows:

Inf > 1.0
1.0 > 0.0
0.0 == -0.0
0.0 > -1.0
-1.0 > -Inf
-Inf > NaN
NaN != NaN

NaN doesn't equal to itself, to check NaN use double.Equals(x, NaN) instead. Extended real is IEEE standard and it is called "floating point". In C#, 2 types for floating point are provided, float and double. Float is single precision, its maximum precision is around 1.4E-45. Double is much precise, its maximum precision is up to around 4.94E-324.

Next post, I will introduce type with unbounded precision.

Dynamic Programming Part III - Partition Function

Partition Function is function to find distinct ways to sum natural numbers to a target number. Such as 4 can be partitioned to 5 distinct ways:

4
3+1
2+2
2+1+1
1+1+1+1

Consider above summation and find overlapping function, we can notice that we can deduct 1 to 4 from target number. If the result is 0, it is the solution. If result is greater than 0, we must do further deduction. And this is the formula of partition function:



Where m is maximum number to deduct, n is the remaining. Whenever n is 0, means it is a solutions. But if n is less than 0, there is no solution for remaining less than 0. We can write above function into following code:

Func<int, int, int> p = null;
p = (m, n) => 1.To(m).Sum(i => p(i, n - i));
p = p.When((m, n) => n == 0, (m, n) => 1);
p = p.When((m, n) => n < 0, (m, n) => 0);
p = p.Memoize();

We can find the partition function of 100 by using following code:

Console.WriteLine(p(100, 100));
//190569292

We can adapt above function to find partition function using a specific set of number. Such as changing £2 to any number of coins (1p, 2p, 5p, 10p, 20p, 50p, 1£, and 2£). Following is the formula.



Where s(i) is the value of a specific item in the set. And now m is the upper bound of the set. We can solve number of solutions of changing for £2 with following code:

int[] s = null;
Func<int, int, int> p = null;
p = (m, n) => 0.To(m).Sum(i => p(i, n - s[i]));
p = p.When((m, n) => n == 0, (m, n) => 1);
p = p.When((m, n) => n < 0, (m, n) => 0);
p = p.Memoize();

s = new[] { 1, 2, 5, 10, 20, 50, 100, 200 };
Console.WriteLine(p(s.Length - 1, 200));
//73682

Next, we can also find the first target number, partitioned by prime numbers, and has over 5000 solutions.

s = new Prime().TakeWhile(x => x <= 100).Cast<int>().ToArray();
Console.WriteLine(1.To(100).First(i => p(s.Length - 1, i) >= 5000));
//71

This post is the end of dynamic programming series. The challenging part of dynamic programming is to find overlapping substructure. Once you find the substructure, your computation of the functions will be extremely fast. Next post is about number which is real number.

Dynamic Programming Part II - Routes

This post is about to give you basic examples and how to solve dynamic programming. A classic dynamic programming example is to find number of routes over a rectangular grid.

Here is example of 2x2 grid, there are 6 routes from top-left to bottom-right (without backtracking).


(pic from projecteuler.net)

Then, how many routes for 20x20 grid? To solve this question with dynamic programming, you must first define the sub-structure. For every point on grid, there is 2 alternative routes, to move down, and to move right. Therefore, current function is a point (m,n), and sub-structure is point on the bottom (m,n-1) and point on the right (m-1,n). Number of routes for point (m,n) equal to point (m,n-1) plus point (m-1,n).

(m,n)-----(m-1,n)
  |
  |
  |
(m,n-1)

if (m,n-1) has 3 routes to destination,
and (m-1,n) also has 3 routes to destination,
then (m,n) will has 6 (3+3) routes to destination

Except point on bottom most, and on the right most, there is only one sub-structure.

(m,0)-----(m-1,0)

then (m,0) = (m-1,0)

and

(0,n)
  |
  |
  |
(0,n-1)

then (0,n) = (0,n-1)

Finally, on the bottom-right most, it is the destination. The route count for itself is equal to 1. And here is the formula:



And you can write it with C# with following code:

Func<long, long, long> func = null;
func = (m, n) => func(m - 1, n) + func(m, n - 1);
func = func.When((m, n) => n == 0, (m, n) => func(m - 1, 0));
func = func.When((m, n) => m == 0, (m, n) => func(0, n - 1));
func = func.When((m, n) => m == 0 && n == 0, (m, n) => 1);
func = func.Memoize();
Console.WriteLine(func(20, 20));
//137846528820

To make it more harder, let's say that each point has different costs, how can we find the route with minimum cost? The logic is the same, but the formula is different. For a specific point on the grid, we will choose route that is lower cost.

(m,n)-----(m-1,n)
  |
  |
  |
(m,n-1)

if total cost for point (m,n-1)=15
total cost for point (m-1,n)=20
point (m,n-1) has lower total cost,
then point (m,n)=15 + cost of point (m,n)

Here is the formula:



And this is code for C#:

int[,] cost = new int[,] {   {131, 673, 234, 103, 18},
                             {201,  96, 342, 965, 150},
                             {630, 803, 746, 422, 111},
                             {537, 699, 497, 121, 956},
                             {805, 732, 524,  37, 331}};
Func<int, int, int> func = null;
func = (m, n) => cost[m, n] + new[] { func(m - 1, n), func(m, n - 1) }.Min();
func = func.When((m, n) => n == 0, (m, n) => cost[m, n] + func(m - 1, 0));
func = func.When((m, n) => m == 0, (m, n) => cost[m, n] + func(0, n - 1));
func = func.When((m, n) => m == 0 && n == 0, (m, n) => cost[m, n]);
func = func.Memoize();
Console.WriteLine(func(4, 4));
//2427

Next article, harder example for dynamic programming.

Dynamic Programming Part I - Introduction

All combinatoric problems can be solved by Brute-force search. But if search space is very large, Brute-force search required very much time and performance to search for solutions. However, we can reduce search space by input the constraints, which is Constraint Programming. And another optimization is to find the pattern of search space, it is Dynamic Programming.

Problems which can be solved by Dynamic Programming, must contains 2 properties, which are

- Optimal Substructure
- Overlapping Subproblems

Optimal Substructure means, the sub-function must return the same solution everytime. For instance,

Start is a problem. The problem can be splitted into 3 sub-problems. Straight lines are known costs. Wavy lines are optimal costs of the sub-problems. If optimal costs is able to determine, the optimal solutions is also able to determine. The minimum cost for this problem is 25 (5 + 20). But if the optimal solutions on wavy lines cannot be determined, then there is no optimal substructure.

Overlapping Subproblems means, the main function must be splitted into sub-function, and all sub-functions should share the same function. For instance, for a Fibonacci number, it is equal to the sum of 2 previous Fibonacci numbers. We can write into function: F(n) = F(n - 1) + F(n - 2). And we must also define the end point of recursive function: F(0) = 0, F(1) = 1.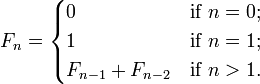



Dynamic Programming in practical makes use of
- Recursion
- Pattern Matching
- Memoization

Recursion is function that can be splitted into sub-function of itself. In C#, it doesn't support anonymous recursive function, we have to set it to null before make the recursion.

Func<long, long> fibo = null;
fibo = n => fibo(n - 1) + fibo(n - 2);

Pattern Matching is to check the input parameter, and reroute to the the appropriate function. For me, I used When method, this method can be found in delegate article, part I, and part II.

fibo = fibo.When(n => n == 1, n => 1);
fibo = fibo.When(n => n == 0, n => 0);

Memoization is technique to cache the result to speed up calculation. Because dynamic programming is optimal substructure, the sub-function can be determined. Memoization is very important to make dynamic programming processes faster. (Memoize method also can be found in delegate article, part I, and part II)

fibo = fibo.Memoize();

Now we can combine it all together.

Func<long, long> fibo = null;
fibo = n => fibo(n - 1) + fibo(n - 2);
fibo = fibo.When(n => n == 1, n => 1);
fibo = fibo.When(n => n == 0, n => 0);
fibo = fibo.Memoize();

Dynamic programming is now completed for Fibonacci function. To call function, is very simple.

Console.WriteLine(fibo(38));
//39088169

Next article, some more examples on dynamic programming.

Roman Numerals

Roman numerals is a numeral system used in ancient Rome. However, today we still use Roman numerals mostly for number-lists, places' year, and on the watches. Here are the letters, which represent a number.

"I" is for 1
"V" is for 5
"X" is for 10
"L" is for 50
"C" is for 100
"D" is for 500
"M" is for 1000

Rule for reading Roman numerals is simple, just sum up value of each letter. However, there is an exception for reduce form. If value of the letter on the left is less than value of the letter on the right, that is reduce form. That letter must deduct from the sum instead of addition. Such as "XLIX", first X is less than L, and I is less than second X. We can write it as -10 + 50 - 1 + 10 = 49.

Rule for writing Roman numerals is also simple. Just deduct from sum by using largest value letter as possible. And you cannot using the letters for 4 times consecutively, in this case, you must write the reduce form. For example 19, Roman number should be "XVIIII" (10 + 5 + 1 + 1 + 1 + 1). But we cannot using I for 4 times consecutively, therefore "VIIII", must be written in reduce form as "IX". As a result, 19 can be written as "XIX".

Now, for coding.

public class Roman {
    int _value;

    public int Value {
        get { return _value; }
    }

    public Roman(int value) {
        if (value < 1 || value > 4999)
            throw new ArgumentOutOfRangeException("value", "value should be between 1 and 4999");
        _value = value;
    }

    public static implicit operator Roman(int x) {
        return new Roman(x);
    }
    public static Roman Parse(string roman) {
        var letter = "IVXLCDM";
        var num = new[] { 1, 5, 10, 50, 100, 500, 1000 };
        var dict = num.WithIndex(letter);

        int value, last = 0, sum = 0;
        foreach (char c in roman) {
            if (!dict.TryGetValue(c, out value))
                throw new ArgumentException("roman contains invalid characters", "roman");
            if (last < value)
                sum -= last;
            else
                sum += last;
            last = value;
        }
        sum += last;
        return new Roman(sum);
    }
    public override string ToString() {
        string numStr = _value.ToString("0000");
        string one = "MCXI";
        string[] five = { "MMM", "D", "L", "V" };
        StringBuilder sb = new StringBuilder();

        numStr.ForEach((c, i) => {
            if (c < '4')
                sb.Append(one[i], (int)(c - '0'));
            else if (c == '4')
                sb.Append(one[i]).Append(five[i]);
            else if (c < '9')
                sb.Append(five[i]).Append(one[i], (int)(c - '5'));
            else //9
                sb.Append(one[i]).Append(one[i - 1]);
        });
        return sb.ToString();
    }
}

If you notice, Parse method uses index injection from previous post, to transform 2 set of array into a dictionary.

To create a Roman number, just assign from integer.

Roman r = 19;

To read Roman number, use Parse method.

Roman r = Roman.Parse("XIX");

To write Roman number, use ToString method.

Console.WriteLine(r.ToString());
//XIX

To get value from Roman number, use Value property.

Console.WriteLine(r.Value);
//19

More example from CodeGolf. Roman to decimal number.

Roman r = Roman.Parse("MCDXL");
Console.WriteLine(r.Value);
//1440

Next article, start a new series topic "Dynamic Programming".

Extension Methods for Enumerable Part II - Index injection and index extraction

In enumerable type, index is useful to identify a member. In C# 3.0, some methods for enumerable provide index parameter such as Select and Where. But most of methods are still not provide index, such as GroupBy and OrderBy.

One of the easy way to inject index into enumerable is to use Closure. For example, if you want to order "ABCDEFG" alternately you may write.

int i = 0;
var e = "ABCDEFG".OrderBy(c => i++ % 2);
Console.WriteLine(e.ListMembers());
//A C E G B D F

To inject an index, you may declare a variable (i) and use this variable as an index in the delegate. You must also put incremental operator (++) to index variable to make index increase every iteration.

Anyway, using of Closure also has drawback. The index variable will not be cleared after enumeration. When you enumerate again index variable will be incorrect. For example:

int i = 0;
var e = "ABCDEFG".OrderBy(c => i++ % 2);
Console.WriteLine(e.ListMembers());
//A C E G B D F
Console.WriteLine(e.ListMembers());
//B D F A C E G

As you can see, the third command and the forth command are the same. But the result is not the same. Because, after run the third command, i value is equal to 7. Then when you call the forth command, the index will be started at index 7 and so on. Finally, the result will not be the same for the second time.

Anyway, this issue can be solved by make the class persistent.

int i = 0;
var e = "ABCDEFG".OrderBy(c => i++ % 2).ToArray();
Console.WriteLine(e.ListMembers());
//A C E G B D F
Console.WriteLine(e.ListMembers());
//A C E G B D F

Above example, we call ToArray after OrderBy method, and make e variable persistent. The result for e will be the same everytime.

Another solution for index injection is to create extension methods.

public static Dictionary<int, T> WithIndex<T>(this IEnumerable<T> source) {
    return source.WithIndex(0.To(int.MaxValue), EqualityComparer<int>.Default);
}
public static Dictionary<T1, T2> WithIndex<T1, T2>(this IEnumerable<T2> source, IEnumerable<T1> index) {
    return source.WithIndex(index, EqualityComparer<T1>.Default);
}
public static Dictionary<T1, T2> WithIndex<T1, T2>(this IEnumerable<T2> source, IEnumerable<T1> index, IEqualityComparer<T1> comparer) {
    Dictionary<T1, T2> dict = new Dictionary<T1, T2>(comparer);
    using (IEnumerator<T2> source_enum = source.GetEnumerator()) {
        using (IEnumerator<T1> index_enum = index.GetEnumerator()) {
            while (source_enum.MoveNext()) {
                if (!index_enum.MoveNext())
                    throw new ArgumentException("index cannot has less length than source", "index");
                dict.Add(index_enum.Current, source_enum.Current);
            }
        }
    }
    return dict;
}

You just call above method before enumeration. The result you get is a dictionary. Key is index, and Value is object. Then after enumeration, you may call Select method to remove index from the object. For example:

var e = from c in "ABCDEFG".WithIndex()
        orderby c.Key % 2
        select c.Value;
Console.WriteLine(e.ListMembers());
//A C E G B D F
Console.WriteLine(e.ListMembers());
//A C E G B D F

You can also pass any kind of index into WithIndex method. The index's length must be greater than or equal to source's length.

For example, you have source and position. And you want to sort source by position. In this case, you can assign position as an index of the source.

var e = from x in source.WithIndex(position)
        orderby x.Key
        select x.Value;

Index extraction is index from specific item in the enumerable. Here is the extension methods:

public static int IndexOf<T>(this IEnumerable<T> source, T item) {
    return source.IndexOf(item, EqualityComparer<T>.Default);
}
public static int IndexOf<T>(this IEnumerable<T> source, T item, IEqualityComparer<T> comparer) {
    IList<T> list = source as IList<T>;
    if (list != null)
        return list.IndexOf(item);

    int i = 0;
    foreach (T x in source) {
        if (comparer.Equals(x, item))
            return i;
    }
    return -1;
}

The example for IndexOf is from CodeGolf. The question is Reverse game. You will get list of numbers randomly. And you must tell how many numbers from the left to reverse. And target is to arrage the numbers.

int[] list = new[] { 8, 9, 4, 5, 1, 3, 6, 2, 7 };

Action<int> reverse = i => {
    if (i > 1) {
        Console.WriteLine("reverse: {0}", i);
        list = list.Take(i).Reverse().Concat(list.Skip(i)).ToArray();
        Console.WriteLine(list.ListMembers());
    }
};

list.Length.DownTo(1).ForEach(x => {
    if (x != list[x - 1]) {
        reverse(list.IndexOf(x) + 1);
        reverse(x);
    }
});
//8 9 4 5 1 3 6 2 7
//reverse: 2
//9 8 4 5 1 3 6 2 7
//reverse: 9
//7 2 6 3 1 5 4 8 9
//reverse: 7
//4 5 1 3 6 2 7 8 9
//reverse: 5
//6 3 1 5 4 2 7 8 9
//reverse: 6
//2 4 5 1 3 6 7 8 9
//reverse: 3
//5 4 2 1 3 6 7 8 9
//reverse: 5
//3 1 2 4 5 6 7 8 9
//reverse: 3
//2 1 3 4 5 6 7 8 9
//reverse: 2
//1 2 3 4 5 6 7 8 9

Above example, you need IndexOf to identify position of the next number you want to reverse in the list. Then you reverse that number to the left, and then you reverse again to move the number to appropriate position.

Next, we will go to Roman Numerals.