Dynamic Programming Part II - Routes

This post is about to give you basic examples and how to solve dynamic programming. A classic dynamic programming example is to find number of routes over a rectangular grid.

Here is example of 2x2 grid, there are 6 routes from top-left to bottom-right (without backtracking).


(pic from projecteuler.net)

Then, how many routes for 20x20 grid? To solve this question with dynamic programming, you must first define the sub-structure. For every point on grid, there is 2 alternative routes, to move down, and to move right. Therefore, current function is a point (m,n), and sub-structure is point on the bottom (m,n-1) and point on the right (m-1,n). Number of routes for point (m,n) equal to point (m,n-1) plus point (m-1,n).

(m,n)-----(m-1,n)
  |
  |
  |
(m,n-1)

if (m,n-1) has 3 routes to destination,
and (m-1,n) also has 3 routes to destination,
then (m,n) will has 6 (3+3) routes to destination

Except point on bottom most, and on the right most, there is only one sub-structure.

(m,0)-----(m-1,0)

then (m,0) = (m-1,0)

and

(0,n)
  |
  |
  |
(0,n-1)

then (0,n) = (0,n-1)

Finally, on the bottom-right most, it is the destination. The route count for itself is equal to 1. And here is the formula:



And you can write it with C# with following code:

Func<long, long, long> func = null;
func = (m, n) => func(m - 1, n) + func(m, n - 1);
func = func.When((m, n) => n == 0, (m, n) => func(m - 1, 0));
func = func.When((m, n) => m == 0, (m, n) => func(0, n - 1));
func = func.When((m, n) => m == 0 && n == 0, (m, n) => 1);
func = func.Memoize();
Console.WriteLine(func(20, 20));
//137846528820

To make it more harder, let's say that each point has different costs, how can we find the route with minimum cost? The logic is the same, but the formula is different. For a specific point on the grid, we will choose route that is lower cost.

(m,n)-----(m-1,n)
  |
  |
  |
(m,n-1)

if total cost for point (m,n-1)=15
total cost for point (m-1,n)=20
point (m,n-1) has lower total cost,
then point (m,n)=15 + cost of point (m,n)

Here is the formula:



And this is code for C#:

int[,] cost = new int[,] {   {131, 673, 234, 103, 18},
                             {201,  96, 342, 965, 150},
                             {630, 803, 746, 422, 111},
                             {537, 699, 497, 121, 956},
                             {805, 732, 524,  37, 331}};
Func<int, int, int> func = null;
func = (m, n) => cost[m, n] + new[] { func(m - 1, n), func(m, n - 1) }.Min();
func = func.When((m, n) => n == 0, (m, n) => cost[m, n] + func(m - 1, 0));
func = func.When((m, n) => m == 0, (m, n) => cost[m, n] + func(0, n - 1));
func = func.When((m, n) => m == 0 && n == 0, (m, n) => cost[m, n]);
func = func.Memoize();
Console.WriteLine(func(4, 4));
//2427

Next article, harder example for dynamic programming.

Dynamic Programming Part I - Introduction

All combinatoric problems can be solved by Brute-force search. But if search space is very large, Brute-force search required very much time and performance to search for solutions. However, we can reduce search space by input the constraints, which is Constraint Programming. And another optimization is to find the pattern of search space, it is Dynamic Programming.

Problems which can be solved by Dynamic Programming, must contains 2 properties, which are

- Optimal Substructure
- Overlapping Subproblems

Optimal Substructure means, the sub-function must return the same solution everytime. For instance,

Start is a problem. The problem can be splitted into 3 sub-problems. Straight lines are known costs. Wavy lines are optimal costs of the sub-problems. If optimal costs is able to determine, the optimal solutions is also able to determine. The minimum cost for this problem is 25 (5 + 20). But if the optimal solutions on wavy lines cannot be determined, then there is no optimal substructure.

Overlapping Subproblems means, the main function must be splitted into sub-function, and all sub-functions should share the same function. For instance, for a Fibonacci number, it is equal to the sum of 2 previous Fibonacci numbers. We can write into function: F(n) = F(n - 1) + F(n - 2). And we must also define the end point of recursive function: F(0) = 0, F(1) = 1.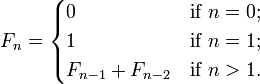



Dynamic Programming in practical makes use of
- Recursion
- Pattern Matching
- Memoization

Recursion is function that can be splitted into sub-function of itself. In C#, it doesn't support anonymous recursive function, we have to set it to null before make the recursion.

Func<long, long> fibo = null;
fibo = n => fibo(n - 1) + fibo(n - 2);

Pattern Matching is to check the input parameter, and reroute to the the appropriate function. For me, I used When method, this method can be found in delegate article, part I, and part II.

fibo = fibo.When(n => n == 1, n => 1);
fibo = fibo.When(n => n == 0, n => 0);

Memoization is technique to cache the result to speed up calculation. Because dynamic programming is optimal substructure, the sub-function can be determined. Memoization is very important to make dynamic programming processes faster. (Memoize method also can be found in delegate article, part I, and part II)

fibo = fibo.Memoize();

Now we can combine it all together.

Func<long, long> fibo = null;
fibo = n => fibo(n - 1) + fibo(n - 2);
fibo = fibo.When(n => n == 1, n => 1);
fibo = fibo.When(n => n == 0, n => 0);
fibo = fibo.Memoize();

Dynamic programming is now completed for Fibonacci function. To call function, is very simple.

Console.WriteLine(fibo(38));
//39088169

Next article, some more examples on dynamic programming.